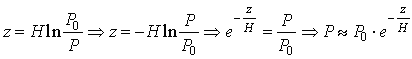La formula ipsometrica
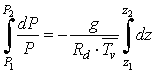 E' una formula che si ottiene combinando la legge dei gas perfetti con l'equazione idrostatica e ci spiega perché la pressione atmosferica decresce in modo esponenziale con la quota.
E' una formula che si ottiene combinando la legge dei gas perfetti con l'equazione idrostatica e ci spiega perché la pressione atmosferica decresce in modo esponenziale con la quota.
Sebbene in modo approssimato per i motivi che illustreremo tra poco, essa descrive la differenza di altezza fra due livelli di pressione (tale differenza si chiama "spessore"). Ricordiamo che:
![]()
dove per il significato dei vari parametri rimandiamo agli articoli precedenti e cioè, rispettivamente, all'articolo sull'Equilibrio idrostatico e a quello relativo all'Equazione di stato dei gas. Se sostituiamo il valore della densità ρ (ricavabile dalla legge dei gas) nella formula idrostatica otteniamo:
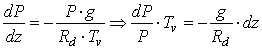
Integriamo ora l'equazione ottenuta fra un'altitudine z1 dove la pressione è pari ad un valore P1 e un'altitudine z2 dove la pressione è P2:
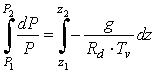
Ciò che possiamo fare è allora prendere il valore medio di Tv nello strato compreso fra z1 e z2. Così possiamo scrivere:
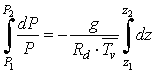
dove il segno sopra Tv sta appunto a ricordare che si tratta di un valore medio e quindi costante per quello strato in un dato momento. Le regole di integrazione ci consentono di scrivere:
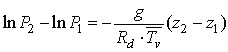
dove il simbolo ln rappresenta il logaritmo neperiano (cioè in base "e"). La differenza di due logaritmi è pari al logaritmo del rapporto dei loro argomenti ed essendo ln(x) = -ln(1/x) si ha:
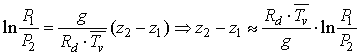
L'approssimazione sulla costanza del valore di g (l'accelerazione di gravità in realtà, seppur di poco, varia con la latitudine e l'altitudine in quanto la Terra è leggermente schiacciata ai poli, dunque la distanza dal centro della Terra cambia in entrambi i casi) può essere rimossa sostituendo alle altezze geometriche z1 e z2 le cosiddette altezze geopotenziali H1 e H2 e continuando a considerare g costante e pari a g0, cioè pari al valore medio al livello del mare (che è 9.81 m/s2). Si veda qui cos'è esattamente l'altezza geopotenziale. Qui ci preme far notare come la formula ipsometrica spieghi l'andamento esponenziale della pressione P con la quota.
Infatti, se al livello del mare (dove z1 = 0) la pressione è P0, posto:
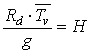
si ha