Equilibrio idrostatico
 Come visto nell'articolo dedicato agli Stati Termodinamici dell'Atmosfera, è un dato di fatto che la pressione atmosferica decresca con la quota. Ma come si spiega tale andamento?
Come visto nell'articolo dedicato agli Stati Termodinamici dell'Atmosfera, è un dato di fatto che la pressione atmosferica decresca con la quota. Ma come si spiega tale andamento?
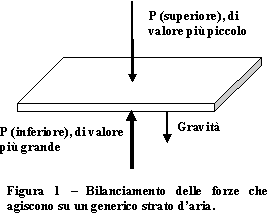
Per capirlo occorre tenere presente che l'atmosfera, nel formare la sottile "pellicola" che avvolge il nostro pianeta, si trova in sostanziale equilibrio tra due forze contrapposte: da una parte c'è la forza di gravità, che tende a "schiacciare" tutta l'aria verso il basso, cioè verso il suolo; dall'altra vi si oppone la forza di gradiente di pressione verticale. Infatti, visto che la pressione aumenta scendendo di quota, allora dato che l'aria si muove da dove la pressione P è maggiore a dove è minore, si stabilirà una forza che tenderà a far salire l'aria stessa, opponendosi alla forza di gravità.
L'atmosfera si trova, dunque, in generale equilibrio idrostatico ("idro" perché è un fluido, "statico" perché è in uno stato "stazionario", fermo). Tale condizione può essere assunta quasi sempre come vera, eccetto se siamo in presenza di forti moti verticali dell'atmosfera (come nel caso di temporali e così via). Ma vediamo più in dettaglio come si arriva ad esprimere matematicamente la condizione di equilibrio idrostatico.
Come detto, lungo la verticale abbiamo a che fare con 2 forze. Iniziamo con il gradiente verticale di pressione. Come si può osservare dalla figura 1, poiché la pressione P diminuisce con la quota, la pressione esercitata sulla faccia inferiore di un generico sottile strato orizzontale è maggiore di quella esercitata sulla faccia superiore. Si ha così una forza
dove ΔP = P(inferiore) - P(superiore) e A è l'area della sezione della colonna d'aria considerata.
Ma sullo stesso "straterello" agisce anche la forza di gravità, che sarà data da
dove g = 9.8 m/s2 è l'accelerazione di gravità al livello del mare (il segno "-" indica che la direzione della forza è verso il basso), m è la massa dello strato in questione. A sua volta, se Δz è lo spessore dello strato e l'aria ha densità ρ, allora m = ρ · V = ρ(A · Δz). Se siamo nelle condizioni di poter trascurare i moti verticali dell'aria, allora dev'esserci equilibrio tra le due forze, ovvero dev'essere:
FP = FG, da cui
ΔP · A = -ρ · A · Δz · g
![]()
Questa è, appunto, l'equazione dell'equilibrio idrostatico dell'atmosfera (il segno "-" indica che la pressione P diminuisce con la quota). Essa ci dice che muovendoci verticalmente da una quota z1 a una quota z2 (quindi Δz = z2 - z1) la pressione deve variare di una quantità ΔP = P2 - P1 che è legata al prodotto tra la densità dell'aria ρ (che tiene conto del "galleggiamento" dell'aria stessa) e g (che tiene conto della gravità).
Così come l'abbiamo scritta l'equazione idrostatica è matematicamente approssimata in quanto è in forma "algebrica" (la cosiddetta "approssimazione alle differenze finite"). Ma se consideriamo, anziché variazioni finite ΔP e Δz, variazioni infinitesime dP e dz (come si fa in quella branca della matematica che si occupa del calcolo infinitesimale) allora il rapporto dP/dz altri non è che la derivata di P rispetto a z. Il significato fisico è lo stesso, ma descrive le variazioni di P rispetto a z punto per punto, anziché "segmento" per "segmento".
Possiamo inoltre osservare come a parità di quota percorsa la pressione decresce con l'altezza maggiormente laddove densità e/o g siano maggiori.
Sebbene l'accelerazione di gravità possa ritenersi costante nella maggior parte delle applicazioni, lo stesso non si può dire per la densità! Ecco che anche qui possiamo capire per quale motivo, per esempio, se c'è aria più fredda e/o più secca (cioè più densa) la P diminuisce più rapidamente con la quota rispetto a zone circostanti più calde e/o più umide (e dunque meno dense).
L'equazione idrostatica è fondamentale in fisica dell'atmosfera e trova numerose applicazioni, come vedremo. Nel frattempo però facciamo un esempio numerico: in prossimità del livello del mare, un aumento di quota di 100 metri a quale diminuzione di pressione corrisponde?
A livello del mare è ρ = 1.225 kg/m3. Posto Δz = 100 m si ha:
ΔP = -ρ · g · Δz = -1.225 · 9.8 · 100 = -1200.5 kg/ms2 = -12 hPa
Naturalmente questa variazione di pressione sarebbe diversa per quote di partenza diverse (cambia ρ) e comunque occorre in generale usare molta cautela nell'impiegare la formula dell'equazione idrostatica nella forma alle differenze finite (che è quella di più facile impiego, in quanto come abbiamo visto può essere risolta con semplici operazioni algebriche). Essendo infatti specialmente la densità molto variabile con l'altezza, l'errore che si commette è tanto maggiore quanto maggiore è l'intervallo Δz impiegato.
Considerazioni conclusive: Oltre a quanto già esposto in questo articolo, ricordiamo che la legge dell'equilibrio idrostatico è usata in molte applicazioni in ambito meteorologico, da sola o in combinazione con altre leggi fisiche (come nel caso dell'equazione ipsometrica, oggetto di un articolo successivo). Essa è in grado di spegare, fra le altre cose, il motivo per cui ad esempio i venti verticali sono spesso più deboli rispetto a quelli orizzontali.