Pillole di Matematica: numeri immaginari e numeri complessi

Pillole di Matematica: numeri immaginari e numeri complessi

Arrivati a questa tappa del nostro particolare viaggio tra i numeri, abbiamo ormai capito che la loro nascita e le operazioni che se ne producono, hanno avuto origine sia da considerazioni teoriche e logiche, sia da esigenze pratiche.

Arrivati ai numeri reali, passando per gli interi naturali, gli interi relativi e le frazioni, ci si accorge che questi numeri non esauriscono ancora tutte le possibilità matematiche e nemmeno le esigenze pratiche. In che senso direte voi? I numeri reali in fondo sono "densi", come abbiamo già avuto modo di (di)mostrare. Cioè tra un numero e un altro ce ne sono infiniti e non esistono "buchi", "vuoti", in quanto si è visto che è sempre possibile far corrispondere ad ogni punto di una retta un numero reale e viceversa.

Tuttavia non è finita. Sono rimaste delle questioni in sospeso, per così dire. Ad esempio sappiamo estrarre la radice quadrata di un qualunque numero, purché nullo o positivo, ma non esiste la radice quadrata di un numero negativo in quanto non esiste nessun numero che elevato al quadrato (o più in generale ad una potenza pari) dia come risultato un numero negativo. O meglio, non esiste nel campo dei numeri reali...

Ma come è successo per altri tipi di numeri, introdotti allo scopo di rappresentare altre quantità o "entità", nessuno ci vieta di allargare il campo e definire nuovi numeri che contemplino anche tale possibilità. Ed è così che si può ad esempio definire l'esistenza della radice quadrata di un numero negativo introducendo i cosiddetti numeri immaginari (in contrapposizione a "reali"). Più precisamente si definisce i = √-1 come unità (immaginaria) di questi nuovi numeri. L'unità immaginaria "i" è quel numero il cui quadrato = -1, cioè i2 = -1. Da qui è possibile definire tutti i numeri immaginari come quei numeri reali moltiplicati per l'unità immaginaria, quindi numeri del tipo "a x i" con a un qualunque numero reale.

Attenzione però ad usare bene l'unità immaginaria, perché essendo definita tramite un radicale ciò può portare ad errori. Ad esempio essendo come detto i2 = 1, si potrebbe scrivere: -1 = i2 = i x i = √-1 x √-1 = √(-1)(-1) = √1 = 1 il che ovviamente è un controsenso. L'errore sta nel fatto che abbiamo effettuato uno dei passaggi con la regola √a x √b = √(ab), la quale regola però è valida solo per numeri reali a e b reali e non negativi...

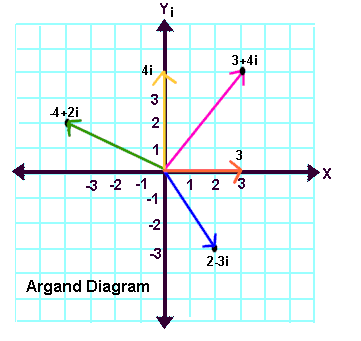
Numeri reali e numeri immaginari possono "unirsi" a formare i cosiddetti numeri complessi, che sono numeri del tipo a + bi, con a e b reali. Quindi come somma di una parte reale (a) e una parte immaginaria (bi). L'insieme di questi numeri forma il campo dei numeri complessi e si indica con C. La corrispondenza "geometrica" non sarà più con una retta, ma con un piano, avendo a che fare con coppie di numeri reali (che in un piano possono individuare punti le cui coordinate sono appunto i due numeri reali che "costruiscono" il numero complesso considerato).

Si potrebbe pensare che a questo livello "inventare" nuovi numeri sia solo un gioco teorico inutile. Si sappia invece che i numeri complessi trovano applicazione in molti campi della Fisica, dell'Elettronica e delle Telecomunicazioni. Può sembrare strano, ma i numeri immaginari (e quindi i numeri complessi) hanno applicazioni molto reali! I numeri complessi costituiscono un nuovo, comodo "algoritmo" per manipolare quantità particolari. Il motivo principale è che molte discipline scientifiche necessitano di entità matematiche note come "vettori". I vettori sono delle "frecce" che hanno una direzione, un verso e una lunghezza. Ad esempio se vogliamo rappresentare in modo completo l'andamento della nostra auto, non ci basta dire a che velocità procediamo, ma dovremo anche dire in che direzione (est-ovest?) e in che verso (verso est o verso ovest?). Ecco, i vettori sono rappresentabili su un piano e siccome anche i numeri complessi lo sono, ecco che può determinarsi un legame fra le due rappresentazioni e tutto ciò che è descritto da vettori in linea di principio può essere rappresentato tramite numeri complessi e viceversa. Quando è conveniente farlo è un altro paio di maniche...

A questo punto in questa sede non entriamo in ulteriori dettagli di come le varie proprietà algebriche e le operazioni matematiche vengono definite in questo caso, anche perché comincia a diventare davvero... "complesso"! Basti ricordare che l'obiettivo resta sempre quello di impostare le cose per fa "tornare i conti".