Pillole di Matematica: numeri irrazionali e numeri reali
Pillole di Matematica: numeri irrazionali ed estensione ai numeri reali
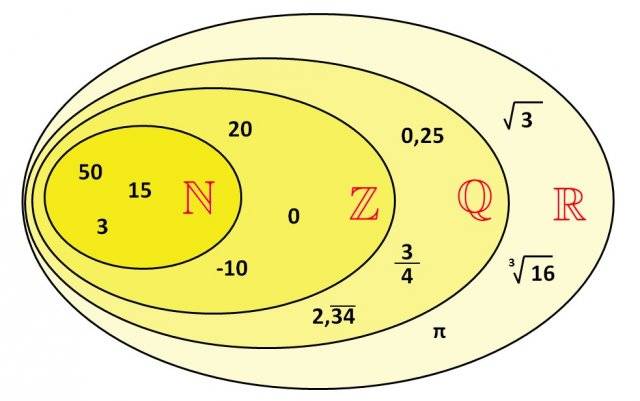Durante il nostro viaggio tra i numeri, ci siamo ad un certo punto resi conto che per rappresentare e far di conto con certe misure o quantità, abbiamo avuto bisogno di introdurre, oltre agli interi naturali, gli interi relativi e le frazioni (o numeri razionali, cioè numeri dati dal rapporto di numeri interi) con e senza segno. In particolare, i numeri razionali danno luogo a numeri rappresentabili senza virgola (gli interi), con un numero finito di cifre dopo la virgola (le frazioni decimali), oppure infinito ma con periodicità (semplice o composta).
Ci si è accorti ben presto che tali numeri non esauriscono affatto le possibilità, né le necessità di calcolo, anche in casi molto semplici. Ad esempio è facile vedere che se prendiamo un quadrato il cui lato è espresso con un numero razionale, allora la sua diagonale non è possibile esprimerla tramite un numero razionale (si dice che le due grandezze, lato e diagonale di un quadrato, sono tra loro incommensurabili e ciò peraltro mise in crisi l'intera scuola pitagorica!).
Infatti, siano L il lato e D la diagonale di un quadrato e supponiamo che il loro rapporto, cioè D/L sia un numero razionale cioè scrivibile come m/n, con m ed n numeri interi. Dato che la diagonale di un quadrato altri non è che l'ipotenusa del triangolo costruito sul suo lato, per lo stesso Teorema di Pitagora abbiamo che D2 = L2 + L2 = 2L2, cioè D2/L2 = 2. Ma per l'ipotesi fatta è anche D/L = m/n e quindi (D/L)2 = (m/n)2 = m2/n2 = 2. Ora, possiamo sempre supporre il rapporto m/n ridotto ai minimi termini (cioè senza fattori comuni), perché se così non fosse possiamo sempre procedere alla semplificazione. Quindi, m2 = 2n2 il che significa che m2 è numero pari (il doppio di un qualunque numero intero è sempre pari) e quindi anche m è pari, cioè è un numero del tipo m = 2p, con p intero. Perciò possiamo anche scrivere 4p2 = 2n2, cioè n2 = (4/2)p2 = 2p2, ma questo significa che allora anche n2 è pari e quindi lo è n. Abbiamo dunque che sia m che n sono numeri pari, contro l'ipotesi di avere a che fare con numeri primi fra loro, cioè contro l'ipotesi che m ed n fossero ridotti ai minimi termini. Siamo arrivati ad una contraddizione e allora dev'essere falsa l'ipotesi che m/n (e quindi D/L) sia un numero razionale. Ne segue che dev'essere un altro tipo di numero, che viene chiamato, proprio perché "non razionale", irrazionale. Sebbene con procedimenti diversi, si può dimostrare che anche il rapporto tra la circonferenza di un cerchio e il suo diametro è irrazionale (il famoso pi-greco!). Del resto ci si poteva chiedere se non potevano esistere, o essere costruiti, dei numeri che abbiano infinite cifre dopo la virgola, ma evidentemente senza alcuna periodicità (altrimenti sarebbero razionali). Ed eccoli qua, esistono eccome, anche in casi concreti.
Questa tecnica di definire i numeri irrazionali tramite le due classi A e B delle approssimazioni per difetto ed eccesso si può estendere anche agli stessi razionali, definendo poi ogni numero reale come una qualsiasi sezione del campo dei numeri razionali.
Si dice che le due classi A e B di numeri razionali formano una sezione del campo dei numeri razionali quando soddisfano alle seguenti quattro condizioni:
1) Ogni numero della classe A è minore di ogni numero della classe B
2) Se un numero appartiene alla prima classe A, ogni numero razionale minore di esso appartiene pure alla prima classe; se un numero appartiene alla seconda classe B, ogni numero razionale maggiore di esso appartiene pure alla seconda classe
3) La prima classe non ha massimo, la seconda non ha minimo
4) Ogni numero razionale, eccettuato al più uno, dev'essere contenuto o nella classe A oppure nella classe B.
Osservazioni: i punti 1) e 2) sono per come costruiamo le due classi. Il punto 3) è perché come abbiamo visto possiamo sempre trovare un altro numero più grande o più piccolo rispettivamente nei due casi. Il punto 4) fa sì che se c'è un numero razionale che viene escluso da entrambe le classi, allora la sezione definisce proprio quel numero razionale (e si dice che la sezione è di 1° specie), mentre se nessun numero razionale è escluso allora stiamo definendo un numero irrazionale (sezione di 2° specie).
Quindi alla fine numero reale è sinonimo di "sezione del campo dei numeri razionali" e si scrive un qualunque numero reale "a" come a = (A,B). In particolare le sezioni di 1° specie definiscono e corrispondono ai numeri razionali, quelle di 2° specie ai numeri irrazionali.
Ovviamente non è questa la sede ed esistono molti testi che approfondiscono l'argomento, ma vogliamo sottolineare il fatto che a questo punto, per essere sicuri e persuasi che i numeri reali, definiti con il concetto di sezione di numeri razionali, siano numeri per i quali è possibile definire le operazioni aritmetiche e algebriche fondamentali e che per essi valgano le solite proprietà formali (commutativa, associativa, ecc...) occorre provarlo. Bene, si dimostra che è effettivamente così, utilizzando la definizione stessa di sezione.
Facciamo solo un esempio: come si definisce la somma di due o più numeri reali? Prendiamo allora due numeri reali (cioè due sezioni del campo dei razionali) quindi h = (A,B) e k = (C,D). Se sommiamo ciascun numero della classe A con ciascun numero della classe C otteniamo una nuova classe A+C. Stessa cosa per B+D. Si dimostra che le due classi così ottenute costituiscono una sezione del campo dei numeri razionali, che possiamo quindi indicare con (A+C, B+D), che tale sezione rappresenta proprio la somma tra i numeri h e k, cioè h+k = (A+C,B+D), che ciò vale anche per la somma di più numeri reali e che l'addizione fra numeri reali così ottenuti gode della proprietà commutativa e associativa.
Una volta dimostrate tutte le varie "situazioni", si vede che tutto l'impianto aritmetico ed algebrico resta perfettamente coerente e funzionante ed anzi ampliato ai numeri irrazionali. In particolare si estendono in generale ai numeri reali anche le potenze, con le dovute eccezioni. In precedenza abbiamo infatti definito le potenze ad esponente naturale e intero e queste potenze si possono effettuare sempre, per qualunque numero reale (eccetto il caso 00, come sappiamo). Ma già nel caso di esponente razionale non sempre si ha soluzione nel campo reale. Ad esempio (-2)(1/2) perché questa non è altro che la radice quadrata di -2, che non ha soluzione nel campo reale. Anche per questo motivo non si definisce la potenza di un numero reale negativo ad esponente reale. Avremmo infatti molte situazioni senza soluzione nel campo reale, come ad esempio (-1,3)2,1 = (-1,3)21/10 = radice decima di (-1,3)21 cioè andremmo a calcolare una radice pari di un numero negativo, che sappiamo non esistere. Esisterebbe invece (-1,3)(3/7) perché andremmo a calcolare una radice dispari di un numero negativo e il risultato è -1,1190072. In generale le potenze ad esponente reale di numeri negativi ha soluzioni nel campo dei numeri complessi.
Ci si potrebbe però chiedere se non sia possibile spingersi oltre e definire non più una sezione di numeri razionali, ma addirittura una sezione di numeri reali. Cosa succede? Niente, perché si dimostra che ogni sezione (A,B) del campo dei numeri (stavolta reali) è di 1° specie, cioè esclude un numero reale che è maggiore di tutti i numeri reali contenuti in A e minore di tutti i numeri reali contenuti in B. In pratica si torna sempre agli stessi numeri reali e questo fatto si esprime dicendo che il campo dei numeri reali è continuo.
Abbiamo finito con i numeri? No, perché come accennato oltre ai numeri reali esistono i numeri complessi...
