Sistemi di riferimento
Le variabili e le relazioni esistenti tra di esse necessitano di una rappresentazione formale che si esplica mediante simboli, formule e grafici. Per farlo, occorre spesso avere a portata di mano un opportuno sistema di riferimento.
Il numero di coordinate da utilizzare per tale sistema di riferimento dipende dalle quantità che si vogliono (o si devono) riprodurre.
Così, se desideriamo descrivere, ad esempio, la posizione e il moto di oggetti nello spazio, avremo bisogno delle tre coordinate spaziali.
Vi sono però vari tipi di sistemi di riferimento, che si distinguono non solo per il numero, ma anche per le caratteristiche geometriche delle loro coordinate. Possiamo pertanto avere coordinate rettangolari, sferiche, cilindriche, eccetera. La scelta dipende essenzialmente dalla convenienza di un sistema o dell'altro secondo le caratteristiche matematiche, fisiche e geometriche di ciò che si vuole rappresentare.
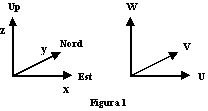
Nel caso si prenda come riferimento la Terra, essendo questa approssimativamente sferica, potrebbe ad esempio essere conveniente l'uso delle coordinate sferiche. In realtà ciò non sempre è necessario. Per una regione sufficientemente piccola come una città o uno Stato, si possono infatti tranquillamente usare le classiche coordinate cartesiane rettangolari, le quali di solito sono chiamate e orientate come illustrato nella figura 1.
Possiamo osservare come le due dimensioni sul piano orizzontale siano indicate con le lettere x e y le cui "frecce" convenzionalmente indicano, rispettivamente, l'Est e il Nord geografico. La coordinata z (componente verticale del sistema cartesiano) rappresenta l'altezza, cioè la distanza dal piano (x,y). Rispetto a tale sistema, dunque, la posizione di ogni punto nello spazio può essere individuato mediante l'insieme di queste tre coordinate.
Al fine di illustrare il movimento di un punto, possono essere indicate anche le componenti della velocità U, V e W, che si fanno corrispondere al moto rispettivamente nelle direzioni x, y e z; ad esempio, un valore positivo di U rappresenta un movimento lungo l'asse x da Ovest verso Est, mentre uno negativo descrive un moto da Est verso Ovest.
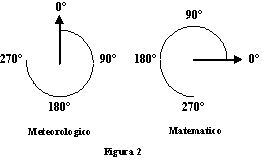Molto usate sono anche le coordinate polari, dove il moto sul piano orizzontale viene espresso in termini di direzione (individuato mediante un angolo α rispetto ad un asse di riferimento) e di velocità (individuata dalla lunghezza M del vettore grafico rappresentativo). Queste coordinate sono costruite su un cerchio la cui rotazione oraria è misurata da 0° a 360° con lo 0° rivolto verso Nord. Tale convenzione è diversa da quella solitamente usata in matematica, la quale prevede una rotazione antioraria a partire dalla direzione dell'asse x (figura 2). Inoltre l'angolo è quello che individua da dove il vento proviene, non la destinazione.
Per passare dalle coordinate (U, V) a quelle (α, M) si possono usare le seguenti formule:
dove α0 = 180° se U > 0, zero altrimenti.
Per passare dalle coordinate (α, M) a quelle (U, V) si possono, invece, usare le seguenti formule:
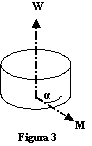
Nelle tre dimensioni spaziali invece delle coordinate cartesiane U, V e W possono essere usate le coordinate cilindriche (M, α, W) dove posizione e velocità di un punto possono essere rappresentate tramite le due coordinate polari α ed M sul piano orizzontale, mentre la componente verticale W rimane invariata, cioè è la stessa di quella usata nel caso delle coordinate cartesiane rettangolari (figura 3).
Considerazioni conclusive: in questo paragrafo abbiamo introdotto i più importanti sistemi di riferimento usati in Meteorologia. L'argomento sarà risultato forse un po' noioso, ma è basilare fornire nozioni indispensabili a chi, dai piloti ai marinai fino a chiunque altro desideri studiare in modo rigoroso una materia scientifica, voglia poi applicare e utilizzare le leggi che governano la Natura.
