Risoluzione orizzontale dei modelli e conversione tra griglia e calcolo spettrale
Risoluzione orizzontale dei modelli e conversione tra griglia e calcolo spettrale
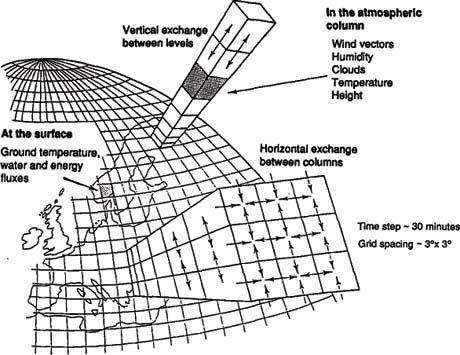
Ogni modello numerico deve poter rappresentare in qualche modo le variabili che si trova a manipolare nelle varie equazioni. Ma come rappresentare l'atmosfera? Sostanzialmente utilizzando 2 tecniche. La prima consiste nel suddividerla in un grigliato tridimensionale, ovvero in griglie orizzontali distribuite in più livelli verticali. Solo quindi in alcuni punti vengono effettuati i calcoli ed è chiaro che più questi sono "fitti" più precisa è la rappresentazione che il modello effettua (ma anche più risorse di calcolo sono necessarie).
La seconda tecnica consiste invece nell'utilizzare una proprietà matematica che consente di esprimere le funzioni in termini di somma (infinita!) di onde (spettro di sinusoidi o di altra forma). Ovviamente non potendo implementare infinite sinusoidi nei computer, occorre "troncare" la somma utilizzando solo le prime "N" sinusoidi.
La "risoluzione" è dunque qui definita in termini o di "spaziatura" oppure di numero d'onda e rappresenta rispettivamente l'area media di ciascun punto della griglia in un modello "Grid-Point" o il numero sinusoidi in un modello spettrale.
Ora, gli elementi più piccoli che possono essere rappresentati con precisione da un modello sono molte volte più grandi del reticolo di risoluzione. Infatti, fenomeni con dimensioni confrontabili alla spaziatura della griglia non si possono rappresentare. Questo implica che se si ha un modello con 10 km di risoluzione orizzontale (la distanza media tra i vari punti di griglia) ciò non significa che si possano risolvere fenomeni di 10 km di dimensione! Un modello con 10 km di risoluzione orizzontale riesce a malapena a rilevare fenomeni con 20 km di diametro e può fare una previsione ragionevole di fenomeni che abbiano una dimensione di almeno 50/70 Km, meglio ancora oltre i 100 chilometri di diametro.
Caratteristiche di piccola o media scala, come ad esempio le celle temporalesche, ce le scordiamo di rappresentarle in questa situazione (possiamo farlo solo con tecniche "indirette", chiamate parametrizzazioni). Ci vogliono infatti circa 5-7 punti della griglia per ottenere approssimazioni ragionevoli delle caratteristiche meteo-climatiche.
Nei modelli spettrali, la risoluzione orizzontale è indicato spesso dal numero "T" (ad esempio, T574), che indica il numero di onde utilizzate per rappresentare i dati. Più precisamente la "T" sta per troncamento triangolare, che indica il particolare insieme di onde utilizzato dal modello spettrale. Oltre il troncamento le onde sono più piccole e rappresentano i dettagli più fini che quindi vengono a mancare (è in un certo senso l'equivalente della mancanza di "infittimento" dei punti nel caso del grigliato).
La "risoluzione" è dunque qui definita in termini o di "spaziatura" oppure di numero d'onda e rappresenta rispettivamente l'area media di ciascun punto della griglia in un modello "Grid-Point" o il numero sinusoidi in un modello spettrale.
Ora, gli elementi più piccoli che possono essere rappresentati con precisione da un modello sono molte volte più grandi del reticolo di risoluzione. Infatti, fenomeni con dimensioni confrontabili alla spaziatura della griglia non si possono rappresentare. Questo implica che se si ha un modello con 10 km di risoluzione orizzontale (la distanza media tra i vari punti di griglia) ciò non significa che si possano risolvere fenomeni di 10 km di dimensione! Un modello con 10 km di risoluzione orizzontale riesce a malapena a rilevare fenomeni con 20 km di diametro e può fare una previsione ragionevole di fenomeni che abbiano una dimensione di almeno 50/70 Km, meglio ancora oltre i 100 chilometri di diametro.
Caratteristiche di piccola o media scala, come ad esempio le celle temporalesche, ce le scordiamo di rappresentarle in questa situazione (possiamo farlo solo con tecniche "indirette", chiamate parametrizzazioni). Ci vogliono infatti circa 5-7 punti della griglia per ottenere approssimazioni ragionevoli delle caratteristiche meteo-climatiche.
Nei modelli spettrali, la risoluzione orizzontale è indicato spesso dal numero "T" (ad esempio, T574), che indica il numero di onde utilizzate per rappresentare i dati. Più precisamente la "T" sta per troncamento triangolare, che indica il particolare insieme di onde utilizzato dal modello spettrale. Oltre il troncamento le onde sono più piccole e rappresentano i dettagli più fini che quindi vengono a mancare (è in un certo senso l'equivalente della mancanza di "infittimento" dei punti nel caso del grigliato).
La lunghezza d'onda della più piccola onda (la più rappresentativa in termini di "finitezza" della rappresentazione) in un modello spettrale viene rappresentata comeminima lunghezza d'onda = 360°/N dove N è il numero totale di onde (il famoso "T"). In realtà le cose possono essere più complicate in quanto alcune caratteristiche vengono comunque calcolate su un grigliato, per poi convertirle nella forma spettrale e in seguito incorporarle nel modello spettrale. Questo introduce errori, che rendono il risultato finale meno esatto di quanto ci si potrebbe aspettare da calcoli effettuati rigorosamente nello spazio spettrale.
Dunque non è facile determinare l'equivalente esatto tra risoluzione orizzontale di griglia e il numero di onde spettrali, proprio perché i modelli spettrali e quelli "Grid-Point" conservano le informazioni in modi diversi. Tuttavia in prima approssimazione si può procedere come segue:
Innanzitutto si assume che k punti di griglia sono sufficienti per acquisire le informazioni contenute in ciascuna serie di onde. Così la formula di cui sopra diventa Δx ≈ 360/(k*N).
Il valore di k cambia secondo la dinamica del modello (Euleriano o Semi-Lagrangiano (o SLG)). Tipicamente k = 3 oppure 2 rispettivamente. Tutto questo purtroppo crea molta confusione nel convertire la risoluzione spettrale in quella di griglia (e anche a seconda se ci riferisce all'equatore o alla latitudine, ad esempio, degli USA o Europea, dove vengono implementati i modelli globali più importanti...). Ma proviamo a fare qualche esempio:
Supponiamo che per un modello euleriano T574L64 (dove cioè si hanno 64 livelli verticali e il troncamento avviene alla 574-esima onda) si abbia k = 3, allora possiamo dire che la risoluzione di griglia "equivalente" è pari a circa:
Δx ≈ 360/(3*574) = 0,20905923°.
All'equatore e per tutti i meridiani (circa 40000 km) ogni grado corrisponde a circa 40000/360 ≈ 111. Perciò moltiplicando il risultato per 111 si ottiene circa 23 km. Ma approfondiamo e generalizziamo ancora di più il discorso. Il raggio (medio) della Terra è circa RT = 6370 km. Quindi la circonferenza di un parallelo a una certa latitudine φ sarà:
Clat = 2πRT * cos (φ)
Dunque una volta calcolato il Δx occorre moltiplicarlo per il rapporto tra circonferenza e 360° per ottenere il "passo" in km alla latitudine considerata. Perciò otteniamo la formula:
Dunque una volta calcolato il Δx occorre moltiplicarlo per il rapporto tra circonferenza e 360° per ottenere il "passo" in km alla latitudine considerata. Perciò otteniamo la formula:
Ris (in km) ≈ Clat / (k*N) = 2πRT * cos (φ) / (k*N)
Nella tabella seguente qualche esempio di calcolo riferito all'equatore (a cui in genere ci si riferisce):
Nella tabella seguente qualche esempio di calcolo riferito all'equatore (a cui in genere ci si riferisce):
| Latitudine | Risoluzione spettrale | Valore k | Risoluzione orizzontale di griglia | Note |
| Equatore (φ=0°) | T574, Euleriano | 3 | 23 km | Modello GFS, da 0 a 8 giorni |
| Equatore (φ=0°) | T190, Euleriano | 3 | 70 km | Modello GFS, da 8 a 16 giorni |
| Equatore (φ=0°) | T1534, SLG | 2 | 13 km | Nuovo modello GFS-FV3(*) a partire dal 12 Giugno 2019! Da 0 a 16 giorni |
| Equatore (φ=0°) | T1279, SLG | 2 | 16 km (**) | Modello ECMWF |
Non entriamo in questa sede nelle problematiche legate alla "geometria" del grigliato stesso, che deve tener conto sia della curvatura terrestre che della chiusura ai Poli. Così come per semplicità abbiamo qui trascurato sia il problema della rappresentazione numerica discreta di variabili e funzioni che in realtà sono continue (ma i computer ragionano solo in termini numerici...) e del loro troncamento (da non confondere con il troncamento spettrale) sia quello della rappresentazione orografica, sia dell'interfacciamento tra i vari livelli verticali...
(*) Con l'introduzione del nuovo core FV3 il sistema di calcolo è diverso da quello illustrato qui
(**) Poi passato a 9 km circa di risoluzione nel Marzo 2016 (https://www.ecmwf.int/en/forecasts/documentation-and-support)
A cura di Fabio F.Gervasi